Je vous souhaite à tous et à toutes une très bonne et heureuse année 2010, qu’elle vous apporte tout le bonheur possible !
De mon côté, je la commence avec mon biscornu à 15 faces, je vous montrerai l’avancée de mon iris demain…, je pense qu’Anne-Lise me pardonnera ce retard…
Je reviens donc à mon biscornu à quinze faces proposé par Véro 21. J’ai donc démonté la face bonne de la ligne d’étoiles, et réassemblé comme la face année, en cousant les bords de l’étoile sur deux lettres différentes. Et voilà un résultat conforme au modèle.
Un profil parfait…
Retrouvez toutes les étapes de ce SAL :
- le contour des quatre premières faces
- le contour des onze premières faces
- la lettre B et les treize premières faces
- la lettre 0 et les quinze faces
- la lettre A
- les trois lettres E
- cinq étoiles
- quatre N
- assemblage des trois premières faces, BON
- les faces Bonne et Année
- questions géométriques
- première version (celle du modèle)
- deuxième version (celle que j’ai choisie finalement)
Après toutes mes interrogations sur des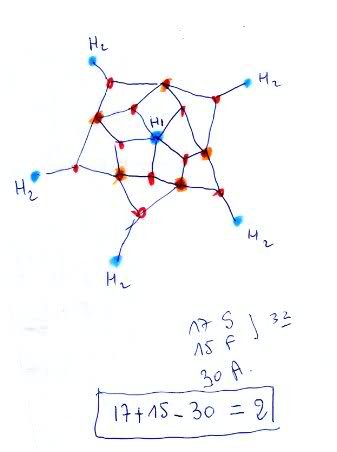 
La première solution, choisie pour la face Bonne, est d’assembler deux bords adjacents de l’étoile à deux bords adjacents d’une même lettre… Même si ici, les arrêtes et les sommets s’assemblent à merveille, je pense que ce n’est pas la bonne solution pour le biscornu, et je ne l’ai pas terminée, j’ai mis des épingles sur les dernières arrètes, je vais découdre et recommencer autrement…
Comment ? Et bien, comme pour la face Année, en cousant un bord de l’étoile sur une lettre et le bord adjacent sur la lettre suivante. Voyez ce que ça donne…
Si l’on regarde sur le côté, pour la première solution, sur le dessus ici, il n’y a pas de déformation des faces des carrés, la couture entre deux faces de lettres vient se positionner dans le creux. Dans le second cas (en bas), la face se déforme pour épouser le creux, et prendre une forme… biscornue ! 
Depuis 
, j’ai quinze faces carrées, impossible en géométrie euclidienne d’en faire un polyèdre régulier à faces planes, et pourtant, le mode d’mploi de l’assemblage me demande de coudre tous les côtés des carrés pour en faire des arrêtes…
.
, kesako ? C’est la première géométrie que l’on apprend à l’école, qui part de cinq postulats, dont le dernier nous intéresse ici, et qui peut se dire soit Si deux lignes sont sécantes avec une troisième de telle façon que la somme des angles intérieurs d’un côté est strictement inférieure à deux angles droits, alors ces deux lignes sont forcément sécantes de ce côté, soit dans un plan, par un point extérieur à une droite, il existe une et une seule droite parallèle à cette droite 
. Un petit tour 
. Vous choisiriez quoi, parmi les 
Une géométrie à courbure constante de type elliptique (géométrie de Riemann, par un point extérieur à une droite, aucune parallèle n’existe) ou à courbure non constante de type hyperbolique (géométrie de Lobatchevski, par un point extérieur à une droite passent une infinité de parallèles) ? Ces différentes géométries, j’y baigne depuis toute petite grâce aux trajets en voiture de la maison au collège et au lycée avec mon père… elles m’ont vallu une très bonne note en philosophie au bac. Il m’a aussi familiarisé aux fractals (j’en ai fabriqué un 
Jusque là, l’assemblage se passe bien, voici Bonne et Année qui devienent… biscornus.
Mais 
Aucune difficulté pour l’assemblage des trois premières faces du biscornu à 15 faces créé par 
Après la 
Elle m’a brodé un joli biscornu sur le thème de la couture…
et l’autre face aussi…
Elle y a joint de quoi ne pas m’ennuyer dans les prochaines semaines, un joli fil, un cœur à broder et une toile Vichy à carreaux bleus…
… et une magnifique carte pop’up/kirigami, quelle finesse dans les découpages ! Un grand merci à toi, 
Jeudi, 
Hier, 
Retrouvez toutes les étapes de ce SAL : 
Cela fait déjà quelques jours que 
Hier après midi,